Vous êtes ici : Accueil > Éducation artistique > Arts visuels > Activités en Arts Visuels > Art & Géométrie
Publié : 28 juin 2011
Format PDF Enregistrer au format PDF

Art & Géométrie

En quoi les arts visuels peuvent-ils apporter leur contribution à l’enseignement de la géométrie, sans pour autant se dénaturer et perdre leur spécificité ?
Comment exploiter tous ces exemples de l’histoire des arts où se mêlent géométrie et peinture, architecture, sculpture... ?
Il ne s’agit pas ici d’habiller d’un voile plus ou moins artistique l’enseignement de la géométrie mais de donner un (autre) sens, au travers des arts visuels, à l’acquisition de ces compétences.

A la recherche des formes géométriques.
 
Sortir de l’école.
Se munir d’un carnet de croquis et d’un crayon, d’un appareil photo et sortir de l’école. Partir à la recherche de parallèles, d’angles droits, de formes et de volumes dans le mobilier urbain et les bâtiments environnants, qu’ils soient d’un intérêt historique et architectural ou non. L’objectif est de rendre familières à l’oeil des enfants toutes ces notions géométriques qui sont la base de notre environnement urbain.
 

Remarque :

Les prises de croquis se font sans outils (équerre, règle…) autre que le crayon. La technique du frottage peut être utilisée (grilles, motifs de plaques...). Il convient de marquer la différence entre « dessin artistique » et « dessin géométrique », sans confusion possible. Ici, nous sommes en situation de dessin pris sur le vif, sans rigueur mathématique ; on pourra toujours, en classe, reprendre ces croquis en situation géométrique, ce qui nécessitera alors un apprentissage technique particulier (dessin technique).


 

Ecole d’Aigurande  : Exemple de travail de modélisation à partir de la voûte en plein-cintre observée sur l’église d’Aigurande : les pièces de la voûte sont fixées au tableau par de la pâte fixante, exceptée la dernière - la clé de voûte - qui tient par son propre poids. L’exercice nécessite de la part des élèves un travail de recherche (par tatônnement) pour bien positionner les deux bases de part et d’autre.

 
 
 Jouer à retrouver les lignes et les formes que les grands peintres ont plus ou moins dissimulées dans leurs tableaux.
 
En demandant aux élèves de rechercher, dans un tableau complexe, les formes géométriques qui président à la composition et la structure interne de l’oeuvre, on favorise une vision plus globale de celle-ci, débarrassée des détails superficiels. Voir le Diaporama des "Formes cachées".
 
Attention : Ne prêtons pas plus d’importance qu’il n’en faut à cet exercice qui consiste à trouver les lignes et les formes cachées. Il convient de le prendre avant tout comme un jeu. De toutes façons, on arrivera toujours à trouver des lignes directrices cohérentes, sans pour autant qu’elles résultent d’une volonté initiale de l’artiste ! 
Il en va de même pour le fameux nombre d’or...
 
Dénicher le Nombre d’Or.
Il s’agit d’un nombre irrationnel correspondant à l’équation x2 = x + 1. Il vaut 
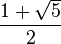
\frac{1+\sqrt{5}}{2}
soit approximativement : 1,618...
Considéré comme la "divine proportion" à la Renaissance, ce n’est qu’à partir du 19ème siècle qu’on commence à parler de "section d’or", puis de "nombre d’or".
 Il est utilisé autant pour ses propriétés algébriques que ses propriétés esthétiques. Phidias l’aurait utilisé pour la construction du Parthénon.
Le rectangle d’or :
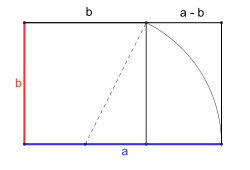
 Ici encore, ne donnez pas aux élèves l’image d’un nombre d’or tout-puissant représentant un idéal esthétique (ce qui est faux). Mais il y a un peu de magie dans ce nombre et dans ses manifestations visuelles - magie à laquelle les enfants ne seront pas insensibles. Il peut donc être intéressant de leur faire trouver des proportions correspondant au rapport 1,618, à l’aide d’une règle et d’une calculette, dans certains tableaux du 17ème et 18ème s. par exemple (niveau CM) .
 
Pour en savoir plus sur le nombre d’or : http://fr.wikipedia.org/wiki/Nombre_d%27or
 
Les avatars du rectangles :
 
Il n’y a pas que le rectangle d’or. D’autres formats sont célèbres :

  • Le format 4/3 : grands panneaux d’affichage ; anciens téléviseurs.

  • Le format 16/9 : téléviseurs à écran plat.

  • Le format 36/24 : diapositives, pellicules photos.

  • Le format international, (L / l = √2 ( ≈ 1,414)  : formats A1, A2, A3, A4, A5… Ce rectangle a la particularité de conserver sa forme quand il est plié en deux sur sa longueur. A0 a une aire d’1 m²  ; A4 signifie que l’on a plié 4 fois le rectangle initial A0.

 
Investir l’espace... le reconstruire.
 
Jeux d’ombres portées : à l’aide d’un projecteur et d’un drap blanc, découvrir toute les possibilités d’agrandissement, de diminution et de déformation sur des formes diverses (avec passage du volume au plan). En projetant sur une grande feuille de papier, on peut ensuite conserver la forme en repassant dessus au crayon.
 
Créer des lignes droites, dans l’espace tridimensionnel de la cour ou de la salle de classe, à l’aide de ficelle ou de fil de laine : les élèves (deux ou trois par fil) tendent des lignes droites découpant l’espace, créent des angles, des points, des intersections, des parallèles et évoluent eux-mêmes dans cet "environnement euclidien" pour le faire varier.
Le rouleau de papier adhésif (servant à délimiter des surfaces peintes) peut être aussi utilisé pour tracer au sol et au mur toutes sortes de lignes (droites) et de segments.
 Cette volonté de se servir du lieu où l’on se trouve pour en faire la matière même de l’oeuvre est une démarche que l’on retrouve chez certains artistes contemporains. Marie-Jeanne Hoffner s’est, entre autre, interrogée sur l’espace et sur la manière de l’appréhender, de le vivre (voir aussi Pauline Kraneis). Ces deux artistes ont participé à une exposition collective "Drawing + Architecture" au collège Marcel Duchamp à Châteauroux. M.-J. Hoffner intervient comme professeur à l’Ecole Municipale des Beaux-Arts de Châteauroux.
 
 
Inventer son propre système plastique.

Construire ses outils géométriques à partir de son propre corps.

A l’instar de l’homme de Vitruve de Léonard de Vinci et du Modulor de Le Corbusier, prendre des mesures de longueurs sur son propre corps (pied, main, doigts, tête, oreille, bras, cuisse…), d’angles (celui formé entre l’index et le majeur quand ils sont écartés, par exemple), des formes (contour de main, doigt, oreille...) afin de se construire un répertoire plastique personnel.

Les outils obtenus peuvent être matérialisés par des bandes et des feuilles de papier. Les enfants peuvent alors construire les formes dont ils ont besoin au moyen de ces "mesures-étalons" et les intégrer dans une production plastique (à plat ou en volume).

La démarche peut être rapprochée (le hasard en moins) de celle utilisée par Marcel Duchamp pour ses "stoppages-étalons".


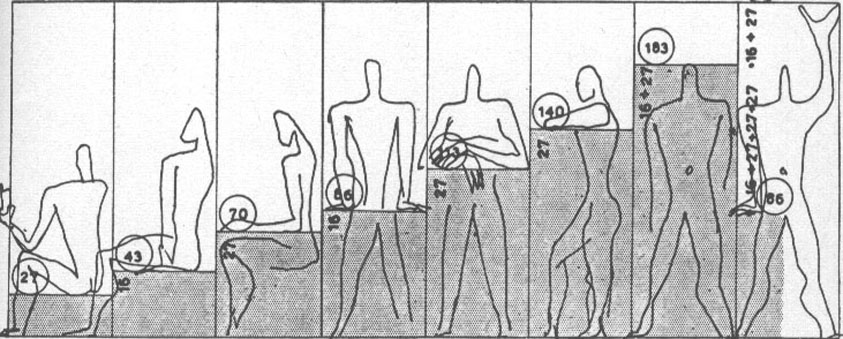
Le Corbusier, Modulor (à noter que le rapport entre deux dimensions voisines correspond au nombre d’or (1,618)

 
 Ces propositions de rencontre entre arts visuels, histoire des arts et géométrie n’ont pas d’autre but que de faciliter une approche sensible de cette dernière. Si on réussit à faire naître chez l’élève l’envie d’aller plus avant dans son projet d’acquisition de ses compétences, ce but sera atteint.
Mais cette rencontre n’est pas en sens unique. On s’aperçoit assez facilement que la géométrie est aussi en mesure d’enrichir les dispositifs que l’on peut mettre en place en arts visuels. Elle nourrit d’un apport théorique non-négligeable la compréhension des oeuvres du patrimoine et laisse entrevoir à l’enfant qu’une démarche artistique, aussi fantasque qu’elle puisse paraître, possède aussi sa part de rigueur.

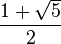
Documents joints